Los problemas de tipo aditivo
El presente trabajo va encaminado a la reflexión sobre la práctica educativa que venimos desempeñando actualmente y de paso incorporar elementos teóricos a nuestra formación y actualización.
La aplicación de problemas de razonamiento con sumas y restas presenta un reto laboral, sobre todo a partir del segundo año de primaria. Como un primer acercamiento debemos de recordar que para realizar las operaciones pertinentes el niño tiene que manejar números.
En este trabajo nos remitiremos a dos tipos de números: Los naturales y los relativos.
LOS NÚMEROS NATURALES no son ni positivos ni negativos. (0, 1, 2, 3, 4…) y representan medidas.
LOS NÚMEROS RELATIVOS sí son positivos o negativos. (…-3, -2, -1, 0, +1, +2, +3…) y representan las transformaciones de los números naturales.
¿Qué es problematizar con números aditivos?
En el libro: El niño, las matemáticas y la realidad: problemas de la enseñanza de las matemáticas en la escuela primaria; escrito por Gerard Vérgnaud (1991), menciona que hay varias categorías de relaciones aditivas o formas de comprender las adiciones (las sumas y las restas), él, sólo trabaja seis en su libro..
De manera breve sólo se mencionan dos categorías:
La primera categoría es cuando dos medidas se componen para dar lugar a otra medida, y se representan con el siguiente esquema:
A + B = C
Esta categoría tiene a su vez dos clases o formas de problematizar.
Aquí es donde empiezan los problemas para el niño, ya que las explicaciones se efectúan como el primer ejemplo de la primera forma de problematizar y cuando les hacemos un ejercicio les incluimos problemas de la segunda forma de problematizar.
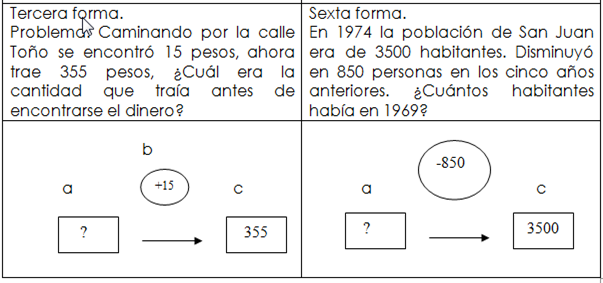
La segunda categoría es cuando una transformación opera sobre una medida para dar lugar a una medida, se representa con el siguiente esquema:
transformación
medida medida
En esta categoría encontramos seis clases o formas de problematizar:
Los esquemas son explícitos y considero que nos ayudarán a reflexionar sobre la forma en como explicamos los problemas a los niños y la forma en como los problematizamos, recordando que aún faltan otras cuatro categorías por estudiar con sus respectivas clases o formas en cada una de ellas, pero un primer paso es adentrarnos en esta propuesta de Vérgnaud.
