El cambio de programa de estudio en educación primaria por el año 1993 trajo consigo un movimiento
para que se entendiera (este importante cambio educativo), se empezaron a realizar cursos,
se entregó material a las escuelas.
Lo anterior viene a colación en cuanto a la entrega de materiales, ya
que en esa etapa se proporcionó un libro (al menos en el Estado de Durango, Méx.) a las
bibliotecas escolares denominado: “El Hombre que Calculaba” de Malba Tahan.
En el texto viene escrito como una interesante cuento, donde el
autor hace gala de su inteligencia al resolver algunos desafíos matemáticos, se
ha elegido algunos para compartirlos y proponer su uso en las clases de
matemáticas, en las llamadas actividades para empezar bien el día o como
variante de los desafíos implementados en las escuelas de tiempo completo o
jornada ampliada.
Iniciaremos entonces con el problema: Los treinta y
cinco camellos que tenían que ser repartidos entre tres hermanos
árabes. Que viene en el capítulo tercero. De manera directa mencionaremos que
el personaje principal del libro (Beremiz Samir), llega a un lugar donde en
acalorada discusión tres hermanos no se ponían de acuerdo para repartirse los
camellos que su padre les había dejado, en las siguientes líneas se transcribe:
—Somos
hermanos, —explicó el más viejo—, y recibimos como herencia esos 35 camellos.
Según la voluntad expresa de mi padre, me corresponde la mitad. A mi hermano Hamed Namur una tercera parte y
a Harim, el más joven, solo la novena parte. No sabemos, sin embargo, cómo efectuar
la partición y a cada reparto propuesto por uno de nosotros sigue la negativa
de los otros dos. Ninguna de las particiones ensayadas hasta el momento, nos ha
ofrecido un resultado aceptable. Si la mitad de 35 es 17 y medio, si la tercera
parte y también la novena de dicha cantidad tampoco son exactas, ¿cómo proceder
a tal partición?
La solución
que da el autor es sin duda muy ingeniosa, también la transcribo para después
ser analizada. En un gesto bonachón, agrega el camello que transportaba a su amigo
ante el asombro de éste y la curiosidad de los hermanos.
—Amigos míos, —dijo—, voy a hacer la
división justa y exacta de los camellos, que como ahora ven son 36. Y
volviéndose hacia el más viejo de los hermanos, habló así:
—Tendrías que recibir, amigo mío, la
mitad de 35, esto es: 17 y medio. Pues bien, recibirás la mitad de 36 y, por
tanto, 18. Nada tienes que reclamar puesto que sales ganando con esta división.
Y dirigiéndose al segundo heredero, continuó:
—Y tú, Hamed, tendrías que recibir un tercio de 35, es decir 11 y poco
más. Recibirás un tercio de 36, esto es, 12. No podrás protestar, pues también
tú sales ganando en la división.
Y por fin dijo al más joven:
—Y tú, joven Harim Namur, según la última voluntad de tu padre, tendrías
que recibir una novena parte de 35, o sea 3 camellos y parte del otro. Sin
embargo, te daré la novena parte de 36 o sea, 4. Tu ganancia será también
notable y bien podrás agradecerme el resultado.
Y concluyó con la mayor seguridad:
—Por esta ventajosa división que a todos ha favorecido, corresponden
18 camellos al primero, 12 al segundo y 4 al tercero, lo que da un resultado –
18 + 12 + 4 – de 34 camellos. De los 36 camellos sobran por tanto dos. Uno,
como saben, pertenece al bagdalí, mi amigo y compañero; otro es justo que me
corresponda, por haber resuelto a satisfacción de todos el complicado problema
de la herencia.
Al parecer fue
un trato justo, es un problema que implica números fraccionarios, trasformación
de fracciones y lo principal, el reparto “aparentemente” dejó a todos
satisfechos… más satisfecho quedó el matemático, imagínense, obtuvo un camello
gratis.
Pero… si se
analiza el reparto, aún y cuando los hermanos obtuvieran sus camellos y se
sacrificara uno para dar la parte correspondiente, de cualquier modo sobraría
un animal ya que no pertenecería a nadie, el padre “aparentemente” repartió su
herencia… pero no el 100% un medio, más un tercio, más un noveno no dan un
entero.
 Lo que
realmente hace es “darle” a cada uno de los tres la parte del camello que se
tendría que haber sacrificado, para eso necesitaba un animal más que pudiera
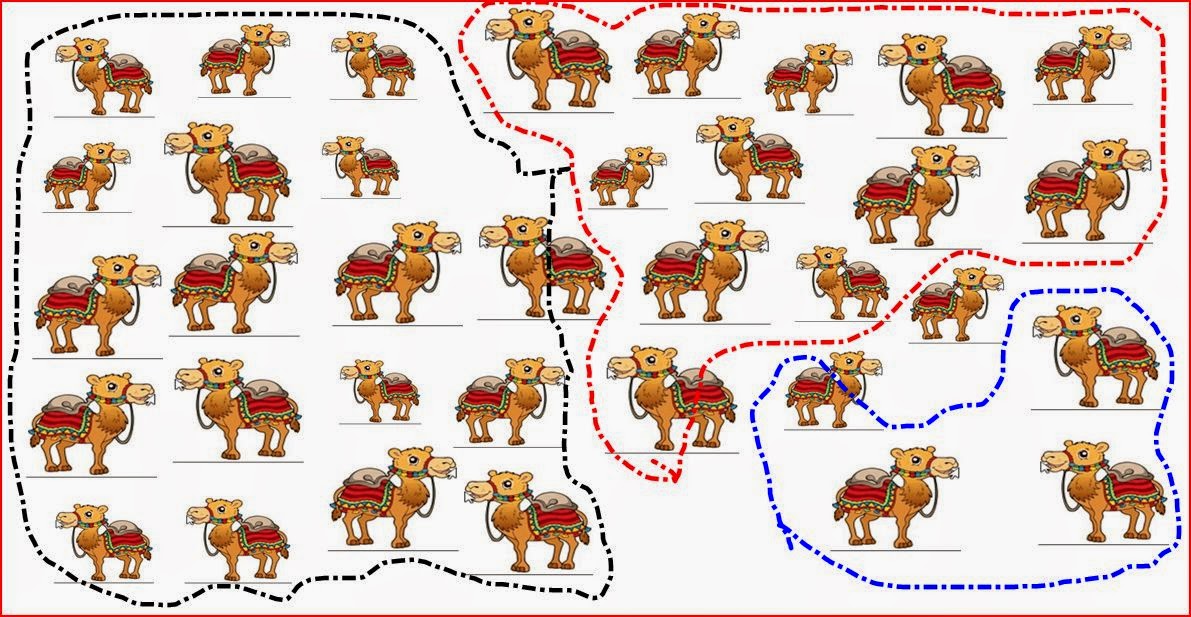
permitir hacer el reparto. En la imagen podemos ver que la suma de los tres
números fraccionarios es 17/18, si se dobla la cantidad
tanto en el numerador como en el denominador obtendríamos 34/36,
si pensamos en ellos como números enteros que representan un conteo (contextos discretos), allí
encontramos los 34 camellos “vivos” (recuerden que en el hipotético reparto
anterior se tenían que sacrificar tres animales), y quedan dos, el que se
ingresó y pertenece al amigo del
matemático y el que siempre sobró.
Lo que
realmente hace es “darle” a cada uno de los tres la parte del camello que se
tendría que haber sacrificado, para eso necesitaba un animal más que pudiera
permitir hacer el reparto. En la imagen podemos ver que la suma de los tres
números fraccionarios es 17/18, si se dobla la cantidad
tanto en el numerador como en el denominador obtendríamos 34/36,
si pensamos en ellos como números enteros que representan un conteo (contextos discretos), allí
encontramos los 34 camellos “vivos” (recuerden que en el hipotético reparto
anterior se tenían que sacrificar tres animales), y quedan dos, el que se
ingresó y pertenece al amigo del
matemático y el que siempre sobró.
Al parecer
para los hermanos no fue buen negocio el no saber sumar fracciones. Lo único
que cambió el matemático es la visión del reparto, podría aplicarse para nosotros
cuando tenemos una forma cuadrada de solucionar problemas de este tipo, de
esto, la necesidad que se busquen soluciones gráficas antes de la enseñanza de las
operaciones.
De paso en
la imagen verde, se hace un recordatorio de cómo realizar sumas con tres
números fraccionarios, encontrando un número común para el denominador. de los
tres números, un medio además de ser fracción común, también es
fracción decimal (con residuo finito), por tanto se puede en dado caso
transformar en número decimal, en cambio las otras dos no, ya que su residuo es
infinito.
Anexo un vídeo sobre el mismo tema:

Esta muy difisil
ResponderEliminardificil es con s difisil
ResponderEliminarJajajaja yo lo resolví en 10 minutos cuando iba en quinto grado 😂
ResponderEliminar