Teniendo en cuenta que entre los reactivos o preguntas de calculo mental del llamado SisAT (Sistema de Alerta Temprana) que se le hacen al niño en la aplicación del instrumento específico para sexto grado está una multiplicación de fracciones, al respecto se elabora este trabajo con la intención de mostrar algunas sugerencias para su aplicación aclarando que en los desafíos se introducen estos conocimientos y para ello el maestro pude observarlos a partir del número 60 para su análisis.
Salvador Llinares C. nos dice en el libro: "Fracciones, Matemáticas, cultura y aprendizaje" que hay una total desvinculación entre el manejo del algoritmo (multiplicación con fracciones) y la resolución de problemas. La necesidad de trabajarlas entonces nos llevará al manejo del modelo de área para su entendimiento y otras situaciones donde pueda aplicarse. Aunque añade que en sí mismo el uso del algoritmo a veces se estime como un procedimiento dudoso, se espera que el maestro cree situaciones didácticas diferentes para trabajar este tipo de contenidos.
Pero vayamos al reactivo -único- de multiplicación de fracciones. Se pide al niño que calcule cuánto es 1/2 X 2/3, es tradicional se enseñe al niño que al multiplicar puede sustituirse la palabra "por" con la palabra "veces" [4 X 5 cuatro veces el cinco = 5 + 5 + 5 + 5] y esto se aplique a la multiplicación de fracción [un medio o una media vez dos tercios]. Decir lo anterior podría desde la argumentación que una media "vez" tendría más sentido si se dice una media o un medio "de" un cuarto y significaría lo mismo. Entonces 1/2 por 2/3 equivale a 2/6 que simplificado es 1/3.
En el ejemplo preparado para esto vemos que incluir por el momento la palabra "de" por "veces" mejoraría el entendimiento desde la pronunciación misma. Fácil es comprender la mecánica desde el cálculo escrito, multiplicar numerador por numerador y denominador por denominador. La imagen hace explicito que un medio de un tercio (donde primero se identifica el tercio) es un sexto del total de la figura.
En el ejemplo de 4 X 5 se comenta que es 4 veces el 5 [5 + 5 + 5 + 5], la propiedad conmutativa nos indica que 4 X 5 = 5 X 4 y nos arroja el mismo resultado 5 veces el 4 [4 + 4 + 4 + 4 + 4] = 20. Tiene sentido la ejecución de operaciones similares pero, ¿sólo operará en ejercicios de fraccionar figuras geométricas?
Si tuviéramos 16 piñas (de pino) y se quiere saber cuantas son en 1/4 de 1/2 del total de piñas. Como ejercicio comprender que se requiere hacer una multiplicación de fracciones [1/4 X 1/2], aunque implica posteriormente ejecutar con el resultado otra operación como se muestra al lado donde al número natural se convierte en fracción impropia, su resultado otra fracción que al ser simplificada nos indica que 1/8 corresponde a 2 piñas. Tomar lo anterior como ejemplo.
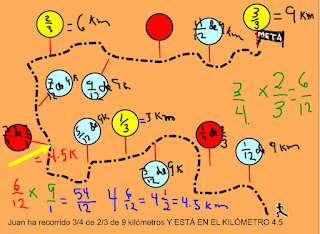En un contexto imaginario podríamos crear una situación didáctica con la siguiente pregunta: ¿Cuántos kilómetros ha recorrido Juan si ya cubrió la distancia de 3/4 de 2/3 del total del camino que mide 9 k? Es obvio que sabemos el resultado... 6/12, simplificada la anterior fracción observamos que es 1/2 y un medio de 9 k son 4.5 k; de la misma manera observamos que funciona como operador tal y como se anota al pie de la figura.
Tal vez tenga sentido las palabras de Llinares al manifestar sus dudas, pero por otro lado algo tenía que surgir al respecto. Espero contribuya lo anterior en algo.
Pero vayamos al reactivo -único- de multiplicación de fracciones. Se pide al niño que calcule cuánto es 1/2 X 2/3, es tradicional se enseñe al niño que al multiplicar puede sustituirse la palabra "por" con la palabra "veces" [4 X 5 cuatro veces el cinco = 5 + 5 + 5 + 5] y esto se aplique a la multiplicación de fracción [un medio o una media vez dos tercios]. Decir lo anterior podría desde la argumentación que una media "vez" tendría más sentido si se dice una media o un medio "de" un cuarto y significaría lo mismo. Entonces 1/2 por 2/3 equivale a 2/6 que simplificado es 1/3.
En el ejemplo preparado para esto vemos que incluir por el momento la palabra "de" por "veces" mejoraría el entendimiento desde la pronunciación misma. Fácil es comprender la mecánica desde el cálculo escrito, multiplicar numerador por numerador y denominador por denominador. La imagen hace explicito que un medio de un tercio (donde primero se identifica el tercio) es un sexto del total de la figura.
En el ejemplo de 4 X 5 se comenta que es 4 veces el 5 [5 + 5 + 5 + 5], la propiedad conmutativa nos indica que 4 X 5 = 5 X 4 y nos arroja el mismo resultado 5 veces el 4 [4 + 4 + 4 + 4 + 4] = 20. Tiene sentido la ejecución de operaciones similares pero, ¿sólo operará en ejercicios de fraccionar figuras geométricas?
Si tuviéramos 16 piñas (de pino) y se quiere saber cuantas son en 1/4 de 1/2 del total de piñas. Como ejercicio comprender que se requiere hacer una multiplicación de fracciones [1/4 X 1/2], aunque implica posteriormente ejecutar con el resultado otra operación como se muestra al lado donde al número natural se convierte en fracción impropia, su resultado otra fracción que al ser simplificada nos indica que 1/8 corresponde a 2 piñas. Tomar lo anterior como ejemplo.
En un contexto imaginario podríamos crear una situación didáctica con la siguiente pregunta: ¿Cuántos kilómetros ha recorrido Juan si ya cubrió la distancia de 3/4 de 2/3 del total del camino que mide 9 k? Es obvio que sabemos el resultado... 6/12, simplificada la anterior fracción observamos que es 1/2 y un medio de 9 k son 4.5 k; de la misma manera observamos que funciona como operador tal y como se anota al pie de la figura.Tal vez tenga sentido las palabras de Llinares al manifestar sus dudas, pero por otro lado algo tenía que surgir al respecto. Espero contribuya lo anterior en algo.
