DESAFÍO MATEMATICO 21... ¿A CUÁNTO CORRESPONDE?... QUINTO GRADO

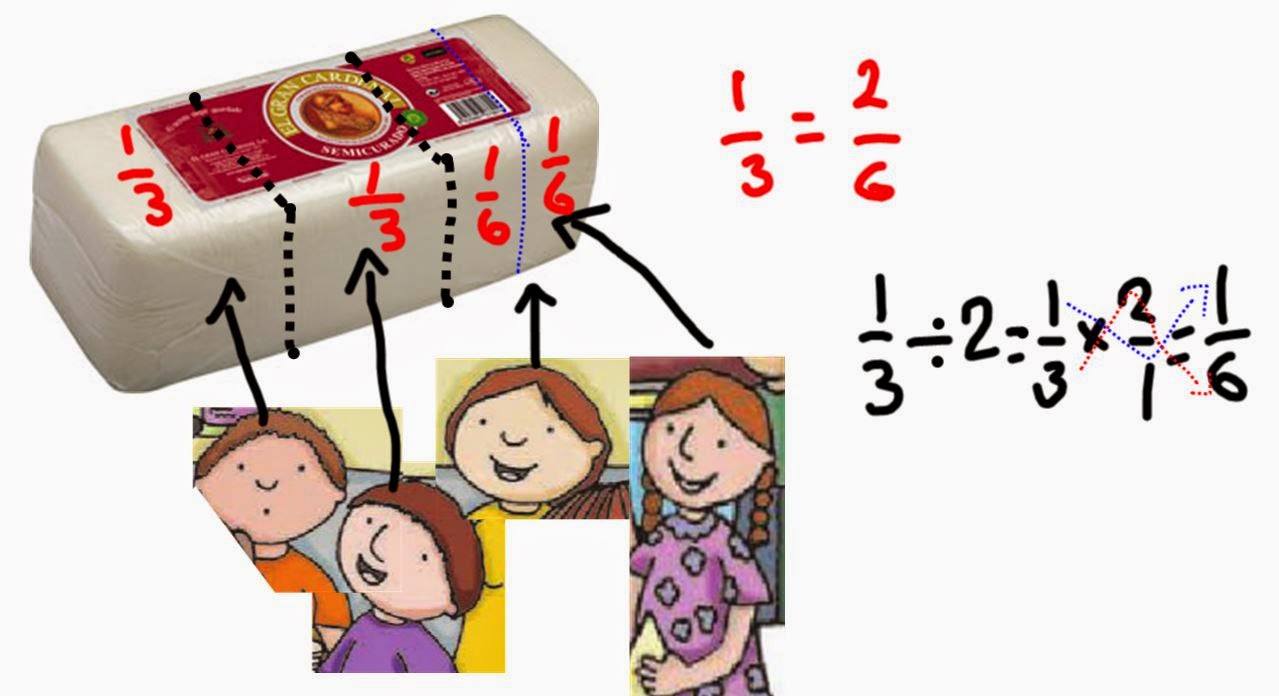
 El desafío matemático 21 está diseñado para la realización de reparto con número fraccionario. El análisis de cada consigna sin embargo merece atención, en el problema uno se plantea el reparto de un queso, siendo una cantidad manejable, creo no debe de representar mucha dificultad. En la teoría entra el juego el concepto de fracción como cociente, es decir, se plantea ¿qué se va a repartir? un queso, la representación se coloca en el numerador del número fraccionario, ¿entre cuantos se va a repartir? Originalmente entre tres niños, por eso el resultado sería 1/3 para cada niño. 

Pero la consigna continúa y se dice que un niño de su parte le regala a su hermana la mitad y en ese sentido viene planteada la pregunta que se espera sea respondida para comprobar que el alumno entendió todo este proceso (y lo realizó... claro) no necesariamente como aquí se describe. Enseguida entonces de debe de hacer el reparto de un tercio entre dos, la figura nos muestra cómo, más económicamente sería decir que la mitad de un número fraccionario es la multiplicación de su denominador por el número de elementos que se van a repartir el queso, pero es necesario que el alumno entienda todo ese proceso y que posteriormente entre sus estrategias encuentre el camino más corto para sus respuestas.

La pregunta dos viene planteada la venta de una casa, el valor sólo es parte del contexto de la pregunta, pero de poco sirve si no se plantean interrogantes respecto a él. Lo que interesa realmente es saber que parte de ese dinero (aunque no la cantidad) representada en número fraccionario corresponde a cada institución a la que se donará el hipotético dinero. en el esquema correspondiente se muestra la forma de llegar a la solución, recordar que no es la única y que cada docente tiene sus propias estrategias al respecto. Como se notará, el resto o se a 2/3 se reparte entre 4 elementos, en este caso instituciones, si se multiplicara el 4 por el 3 que es el denominador se obtendría 12 y conservando el 2 del numerador sería 2/12 que equivale a 1/6, insisto esto sería la forma económica pero no a la que llegan todos los alumnos, de allí a realizar estrategias variadas para hacer comprender al niño.

Si observamos la pregunta tres, la consigna maneja tres momentos en los que se emplear un tiempo indefinido ya que no indica ni su comienzo ni su fin, puede ser de una semana a un mes, un año o varios. Lo importante es que se entienda hay tres momentos que se pueden representar de manera abstracta, a diferencia del problema anterior que se manejan elementos abstractos (una persona y cuatro instituciones) también susceptibles de abstraerse. A saber la consigna indica que para el primer momento se empleará la mitad del tiempo, por tanto, para los otros dos momentos se usará la otra mitad, y una mitad dividida entre dos momentos, siguiendo con la estrategia de multiplicar numerador con elementos y conservando el numerador obtenemos 1/4. Cada momento restante tendrá un cuarto de duración, la pregunta solicita saber sólo uno de esos momentos, en este caso el tiempo dedicado al estudio de la cultura.

Habrá notado el lector que se puede aprovechar para hacer otra serie de cuestionamientos en las consignas anteriores como: qué fracción de tiempo se ocupó Bety en estudiar el hebreo y viajar; o del dinero que se quedó la persona, lo reparte entre tres sobrino, que fracción le correspondería a cada uno de los sobrinos o qué cantidad de dinero le daría a cada uno... bueno eso depende del tratamiento que se realice al tema.

                                                                                                                                                               

Para el problema del festival del pueblo se hace una sugerencia similar a las anteriores para sus solución, se observan tres rubros en los que se reparte cierta cantidad de dinero, que en realidad no importa cuánto sea... de los tres rubros, uno, el de bebidas y otros se subdivide entre cuatro rubros, en ellos se plantea el trabajo, si es un tercio lo que ahora se va a dividir entre cuatro y se multiplica directamente 3 x 4, se obtiene 12, conservando el numerador de un tercio, el resultado es 1/12, como dos rubros son bebidas (aquí debe tener cuidado el alumno de entender que las aguas y los refrescos entran en bebida), y eso es la pregunta, entonces 2/12 sería la respuesta. Los esquemas espero sean auxiliares para este ejercicio, sin leer el libro para el docente se hace las siguientes aportaciones, pero en sus reuniones pueden comentar las diferentes maneras en cómo transitó este ejercicio con sus alumnos. Espero sea de utilidad y realicen comentarios al respecto.

DESAFÍO MATEMÁTICO 24... ¿QUIÉN VA ADELANTE?... SEXTO GRADO

El antecedente de este desafío 24 es el 8 el equipo de caminata en el mismo libro de sexto grado. La diferencia es que en el número 8 se plantea un recorrido en circuito, para el ejercicio presente se plantea la situación problemática en una distancia hipotética de 5 kilómetros rectos. 

Para eso sugerimos emplear entonces una tabla como en dicho desafío o seguir la indicación del libro de dibujar una recta y dividirla en quintos… anticipa el libro para el docente que si algún alumno realiza una recta y toma como base el cuaderno rayado, se le pida que explique el porqué lo realiza así para que el resto de sus compañeros lo imiten.

Siete son los personajes participantes, en la tabla construida se representa imagen de cada uno, empezaremos con el campesino, se indica la distancia recorrida, su avance fue de ¹/₃ de distancia. 

Para trasformar a kilómetros se sugiere tomar como operador la distancia total, en este caso el número 5. Se debe entender como “cuánto es un tercio de la distancia, esto es, de 5 kilómetros”. Se observa el proceso en la figura aunque en la división sólo se obtiene un decimal, es recomendable en los grados de quinto y sexto encontrar hasta dos decimales en una operación.

El estudiante de bachillerato se indica que recorrió 0.8 de la distancia, la operación más económica está indicada con el número uno, y se agrega el mismo proceso seguido con el campesino, pero antes se realiza una transformación de número decimal a fracción decimal. 

En ambos caso se comprueba el mismo resultado y a la vez se sabe el avance que tuvo el alumno de sexto grado cuyo dato conocido era que había recorrido 4 kilómetros.

Para conocer en cuantos kilómetros se traduce el avance del ama de casa procedemos de igual manera que en los casos anteriores, y se resuelve de paso cuánto recorrió Mariano, el alumno de primaria, aquí es conveniente permitir el análisis de que ¼ es equivalente al número decimal 0.25, para ello permitir que los alumnos agoten sus posibles respuestas y guiarlos hacia dicha conclusión.

Para saber cuánto recorrió la enfermera, se puede el alumno fijar lo que avanzó el ama de casa y multiplicarlo por tres o sumarlo tres veces, bueno hay mucho de donde pueda tomar de base. 

Lo importante que la tabla sea una buena estrategia para primero conocer lo que han recorrido cada personaje y posteriormente responder las preguntas del desafío.

Nos quedaría conocer la distancia transitada por el ganadero, se espera que al igual que se hiciera con el ama de casa y el alumno de primaria, se identifique lo recorrido entre ganadero y estudiante de primaria como igual. Entender que el número decimal 0.8 y el número fraccionario ⁴/₅ son equivalentes por tanto serían tres los personajes que trotaron la misma distancia.

En las consignas se habla de tercios, cuartos, quintos y décimos, podría emplearse rectas con dichas medidas y tratar de entender mejor gráficamente hasta donde recorrió cada personaje teniendo siempre presente la distancia total.

Recuerde que lo anterior es sugerencia (no pedida, por cierto) para dicho ejercicio. Espero comentarios.

DESAFÍO MATEMÁTICO 20... EL MÁS RÁPIDO... SEGUNDO GRADO

En el libro para desafíos matemáticos de segundo grado, en la lección 20 se plantea un ejercicio que privilegia el uso de operaciones aditivas. Está diseñado para que se encuentren las soluciones de manera mental (sin usar lápiz, papel o algún otro material) y que colectivamente se expliquen las mejores formas de encontrar las respuestas a cada uno de las tareas.

En la figura de enfrente se muestran los ejercicios con su respectiva pregunta. La respuesta que más se repita —según las consideraciones previas—  probablemente sea la respuesta correcta, los alumnos que las emitan serán quienes expliquen sus procesos, así se prevé en el libro para el docente.

Qué pasará en caso de que la mayoría de las respuestas no sean correctas. Lo interesante sería de cualquier modo conocer los procesos que siguió cada alumno para hacer ajustes y replantear las preguntas.

Para un grupo multigrado, sería interesante trabajar el ejercicio de manera abierta… para todos o al menos para los de segundo, tercero y cuarto. El papel del docente sería de inducir al alumno para que ejecute mentalmente las descomposiciones aditivas. Veamos la primera pregunta, se espera que el alumno  logre “desbaratar” los números ya sea 40 + 10 + 3 y que aplique una de las cuatro propiedades de la suma y se recalca la suma pues es el tipo de operaciones más adecuada y económica… la propiedad distributiva podría ejecutarse así: (40 + 10) + 3…

Esperando que no haya complicaciones, de cualquier manera se recomienda (al docente) el análisis del problema según la clasificación de Gérard Vergnaud. La primera pregunta remitiría a la clasificación de transformación; se entiende un proceso de tiempo en el contexto del planteamiento… de una cantidad inicial que tenía antes del juego o competencia y la pregunta de cuantas tiene en ese ahora final, ese después de jugar. La cantidad que ganó, ese incremento positivo introduce una cantidad relativa que transforma (segunda categoría) la cantidad inicial. En ello debe de pensarse también.

Ya de lleno en el tema, vamos a referirnos a la segunda pregunta. La descomposición ideal sería: 50 + 30 + 5 + 5 y su distribución (50 + 30) + (5 + 5)   (80 + 10). Y bueno, comparar con la pregunta uno y ver que cae dentro de la clasificación de transformación… se percibe un antes, un durante y un después.

En la cuarta pregunta la descomposición esperada y posterior distribución es: (30 + 20) + (5 + 5). Ya distinguido que en las explicaciones anteriores se está abordando el estudio de las categorías aditivas de Vergnaud, se señala que este problema se inserta en la primera categoría pues claramente se percibe cómo se unen dos medidas para hacer un todo. Teóricamente es de los primeros que se deben de enseñar a los alumnos.

Los problemas donde se usan números naturales que representan medidas son idóneos para desarrollar la noción de adición y sustracción… cómo, con la sustracción se podría trabajar replanteando la pregunta, un cambio sería: En dos botes hay 60 canicas en total, si uno contiene 35, ¿cuántas canicas contiene el otro bote? Sustrayendo o complementando se obtendría la respuesta (ver Vergnaud p. 178, El niño las matemáticas y la realidad). Respetando la estrategia propuesta en esta lección se haría la descomposición (60 – 30) – 5 para la sustracción ó 35 + (5 + 10 + 10)= 60 para la complementación.

Los problemas uno y dos se concluye caen o pertenecen a la segunda categoría pues al momento de redactarse: “ganó” y “llegaron” modifican como ya se dijo antes a la cantidad inicial, en la pregunta cuatro las cantidades ya están establecidas en “partes” y sólo se quiere encontrar el “todo”. 

La pregunta cinco nos llevaría a una descomposición sencilla: 10 + 5 + 10 + 2; su distribución (10 + 10) + (5 + 2)… y en cuanto a insertarlo en alguna de las categorías, aparentemente sería parte de la primera.las palabras claves que nos harían considerar lo anterior son: “le dejaron” y la pregunta traslada a un tiempo futuro, se quiere saber cuántas palabras “escribió” Ana, por tanto se considera que son números relativos y se inserta en la cuarta categoría.

La pregunta más difícil, coincidiendo con las indicaciones que vienen en el libro para el docente, es la tres. El alumno debe de echar mano de la memorización de resultados para darse cuenta que hay dos procesos en el mismo contexto; por un lado incorporar a su proceso mental que un niño “comió” una cantidad específica de un producto, el acto de comer indica que de “x” producto hay -25 piezas y que una niña come la misma cantidad que el niño (-25) y otras 22 más… pero que en la práctica son un decremento (-25) + (-22).

Como estas cuestiones teóricas no llegan hasta el alumno, económicamente (se espera) que entienda, recuerde o asocie que la niña comió primero 25 (igual al niño) más 22 de un jalón y llegue a la conclusión de que el buen gusto por las pasas la hizo consumir la cantidad de 47. Fácil verdad… bueno además se espera que brinque el escollo con la descomposición aditiva de 20 + 5 + 20 + 2 y asocie (20 + 20) + (5 + 2) o siga descomponiendo 10 + 10 + 10 + 10 + 5 + 2… pero bueno, estamos divagando.

Ojalá algunos compañeros hayan transitado este desafío de manera exitosa, sin contratiempos, y tengan la oportunidad para comentarnos sus procesos. Recordando que este ejercicio está diseñado para realizar cálculos mentales y empleen estrategias de descomposición y aplicación de alguna de las propiedades de la suma o resta, no estaría de más reformular los problemas y hacerlo de manera escrita… sugerencia no pedida… que se trabaje con planteamientos de la primera y segunda categoría, más con la primera hasta que las dominen (los alumnos) y tener cuidado si su alumnos ya están capacitados para adentrarse en planteamientos de la tercera y cuarta categoría. Por cierto, la pregunta cinco en que categoría la ubicarían ustedes… primera o cuarta.

Espero sus comentarios.

DESAFÍO MATEMÁTICO 2... ¿SUMAR O RESTAR?... QUINTO GRADO

En el desafío matemático número 2 del libro de quinto grado, se presenta una lección donde es necesario realizar o sumas o restas de números fraccionarios. En las consideraciones previas en el libro del docente inicia diciendo: “Se espera que los alumnos resuelvan los problemas con relativa facilidad…” o sea, condicionado a que debe ser fácil su resolución pero hay que observarlos por si cometen errores también se sentencia. Nada tan aventurado decir lo anterior, sobre todo si las fracciones según han manifestados los compañeros de la Zona Escolar 80 en Durango ha sido uno de los aspectos más difíciles de tratar.

En la lección vienen tres consignas, la primera alude hipotéticamente a encontrar el faltante de una cinta adhesiva. Digo hipotéticamente porque se debe confiar que la cinta mida eso pues en la práctica o para hacerlo práctico sería difícil desdoblar una cinta así… es recomendable realizarlo físicamente, pero bueno, viendo eso, se privilegia el manejo de las fracciones, es decir, hacer cuentas ya sea sumando o restando.

Yendo al problema, se sugiere en este grado ir directamente a las palabras del problema para entender la tarea, independientemente de saber sumar o restar con números fraccionarios, se puede analizar la intención y enfatizar el verbo clave. 

Dice: “ocupé”, los sinónimos pudieran ser muchos… tomé, gasté, usé, corté… qué parte ocupé, 2 ¹/₃ ó ³/₆. Una vez establecido o  entendido lo que  se gastó, cortó o usó, en este caso ³/₆ se puede lanzar o prever que la incógnita o respuesta deseada debe ser menor que 2 ¹/₃. Bien, esta consideración previa —no pedida—, se hace necesaria en un contexto donde se manifiesta que los niños no entienden lo que leen. La operación ideal, esperada, deseada… es que entienda el alumno que restará a 2 ¹/₃ los ³/₆ que “ocupó”. 

Pero acudiendo al esquema donde el todo es el resultado, se podría analizar que la parte ocupada es una medida, y la parte no-ocupada sería otra medida y ambas suman el todo inicial como muestra la figura siguiente. 

Nos llevaría a entender que la parte no-ocupada es una medida en cierto sentido relativa y con esto inferimos la necesidad de usar una transformación pues se da un devenir en el problema (lo que había antes “la cinta completa”, lo que se “ocupó de la cinta” durante el día o momento “sobró de la cinta” y que responde la pregunta planteada, esquema de la figura de enfrente.

En la segunda y tercera pregunta si queremos analizarla como un todo, se necesitaría un esquema de tres medidas de las cuales una sería la incógnita planteada.

Como en este espacio se recomienda si no sacar a los alumnos para que escenifiquen o hagan grupos que representen a los alumnos, se realicen al menos dibujos de niños y que los grupos permitan hacer repartos exhaustivos, es decir, en la pregunta uno se tenga o no se tenga una cinta o cuerda para cortarla, la imaginación acepta la acción de tijeretear una cinta, pero en el caso de personas no se podría hacer eso o saldría de la lógica de un alumno repartir partes de un niño. 

Qué cantidad se necesita para que opere el problema 2, se necesita mínimo un grupo de 6 niños y a partir de allí sean 12 ó 18 ó 24… para que se pueda repartir sin imaginar que se corte el cuerpo de un alumno.

Para la pregunta tres se requieren lo mismo, fijarse que si se representa al grupo con dibujos o niños, cuidar los repartos y no salir con la sorpresa de que a alguien se debe de cortar.

Aparentemente el desafío se encamina a elegir sumar o restar, pero son dos situaciones distintas, la primera donde se muestra un todo (la cinta) que real o imaginariamente se puede cortar, y las situaciones de las aulas, al no establecer o dejar espacio para asignarle un número de elementos a los conjuntos o grupos (porque ya vimos que no cualquier número de elementos se prestarían para "partir" en tercios, medios o sextos). 

Esos pequeños detalles deben alertar que las situaciones donde se quiera fraccionar deben ser claras. Queda también la advertencia que se hace en el libro para el maestro del uso de fracciones propias y mixtas, en sí son muchos detalles a cuidar, pero poco a poco se deben de ir superando. Y se vuelve a recomendar, el uso de material tangible o mediante dibujos puede ayudar mejor al alumno a comprender las situaciones planteadas y por tanto resolver los desafíos.