DESAFÍO MATEMÁTICO 10, SEXTO GRADO... LA MERCERÍA

En este desafío se puede entender que entra dentro de la categoría de problemas de tipo multiplicativo (isomorfismo de las medidas). Dos dimensiones o medidas se encuentran presente en su historia, por una parte la medida de encaje o listón y la segunda medida de dinero. Es pertinente reconocer que el manejo numérico representando cantidades de dinero y longitud con enteros y fracciones se presta en el ejercicio en cuestión.

La correspondencia entre las medidas se hace de manejo sencillo con el esquema propuesto en el desafío 17 también de sexto grado ya que de entrada al leer la tarea nos señala claramente el valor unitario de cada producto. 

Además la colocación de la incógnita permite sólo emplear multiplicaciones y no combinado con divisiones como lo exigiría en otros planteamientos la colocación de las cantidades y x.

En las consideraciones previas del libro para el docente se hace la propuesta de realizar multiplicaciones mediante descomposiciones, es una estrategia adecuada y lo propuesto aquí es eso, otra simple propuesta (no pedida) que espero al lector le sirva y adecue a otros ejercicios similares.

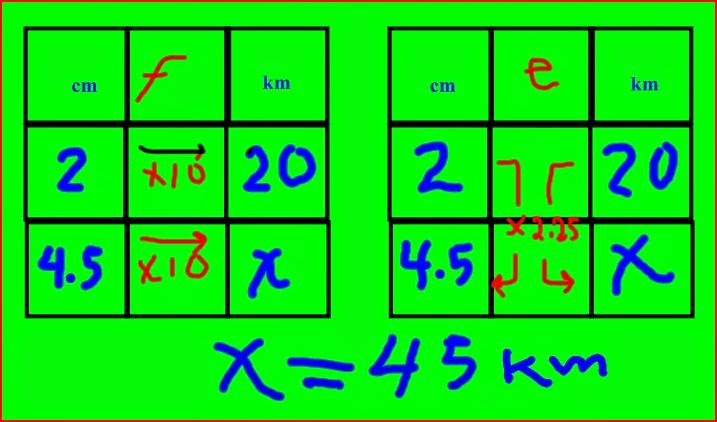
Podemos describir el proceso en las dos formas; mediante una multiplicación del factor (de manera horizontal)  entre la unidad de medida de longitud (metros) por el valor en pesos de la unidad de medida anterior. Entender como factor pues nos permitiría entender por qué una unidad de medida (A) al operar se transforma en otra unidad de medida (dinero) que se corresponden.

Independientemente de la intención para esos días de clase del profesor de grupo, se puede realizar esa descomposición si además requiere reafirmar procesos distintos de multiplicar, sumar, restar o dividir que se presentan en la trama total de las dos historias o de manera más económica usar la calculadora cuando se ha apropiado del proceso propuesto.

En el texto se quiere entender, y así lo afirma el libro para el docente en el segundo problema o tarea donde pide encontrar cuánto sobrará de los 40 pesos que le dio la mamá a Guadalupe y le indica al docente que le falto 1.80 pesos para su encargo… pero aquí me cuestiono de toda la trama o historia de este desafío, acaso Guadalupe no está en la tienda comprando encaje como se detalla en el primer problema o consigna y después como ya vimos, se lee “también pidió  4.75 m de cinta azul…” entonces algún alumno puede interpretar que quiere comprar los dos productos con los 40 pesos a menos que para el encaje llevara otra cantidad.

Las estrategias que un alumno puede aprender y aplicar en la resolución de problemas no tiene fronteras como las que aquí de manera convencional se muestran, el tener un apartado para problemas de tipo aditivo y ahora estas de tipo multiplicativo se hacen queriendo tener un orden, este ejercicio se resuelve o al menos algunos de sus pasos son salvados mediante el empleo de estrategias propias de los números fraccionarios ya que estamos empleando números decimales finitos en uno de las dos dimensiones de medidas (metros). Pero en fin se espera que sea de utilidad lo aquí trabajado, principalmente sea de apoyo para mis compañeros de escuelas multigrado.

DESAFÍO MATEMÁTICO 17 SEXTO GRADO... ¿CUÁL ES LA DISTANCIA REAL?... PROBLEMAS DE TIPO MULTIPLICATIVO

En los problemas de tipo multiplicativo, la historia o trama que encontramos en cada planteamiento arrojan una relación de cuatro elementos (relación cuaternaria) que se corresponden mutuamente y por tanto clarifican esquemáticamente los datos para encontrar respuesta a la interrogante de cada problema. En esta serie de aportes, se seguirá acudiendo a la teoría de Vergnaud (2003) quien escribió al respecto y a los autores que lo retoman en sus textos e interpretan y enriquecen sobre el contenido de sus ideas.

Por relaciones multiplicativas se entenderá como la ejecución de una multiplicación o división al resolver una situación problemática y enfocada a solucionar la pregunta específica que se plasma en una trama hipotética o real de un desafío donde intervengan datos. La primera forma o relación multiplicativa que aborda es la llamada isomorfismo de las medidas, estos términos sin adentrarnos mucho en su análisis semántico diremos que corresponde a una igualdad de formas o dicho de otra manera a una correspondencia entre dos medidas distintas ya sea en cantidad de un tipo con otro… es una correspondencia perfecta uno a uno que ya se ha visto principalmente en el análisis de tablas de variación proporcional directa.

Se entiende pues que entran en juego cuatro cantidades y dos tipos de medidas, a cada tipo por tanto dos cantidades, en el transcurso de este escrito deducirán lo anterior. Para buscar esa utilidad se pretende enlazarlo con los ejercicios de desafíos matemáticos que se están trabajando actualmente como textos de trabajo en la escuela primaria de México; en esta ocasión se analiza el desafío 17 sexto grado y se aclara que va con la intención de ser un apoyo al docente sabedor que tiene un auxiliar que le muestra cómo afrontar didácticamente dichos trabajos.

Para responder a los planteamientos del ejercicio 17 referente al cálculo de la distancia entre cerros, se pide en las consideraciones previas del docente abordar o analizar el segmento del libro y la distancia que representa, claro está que debe ir directo a medirlo, para efectos de comprensión, con algunos programas en la figura se muestra que representó el segmento con una medida de dos centímetros, por tanto dos centímetros será igual a 20 kilómetro (y un centímetro a 10 kilómetros) como se muestra en una de las tablas, allí se lee en color rojo las cuatro cantidades y los dos tipos de medidas. 

Las cantidades por el tipo de medidas centímetros son 2 y 1.5, el dos representa la medida del segmento y 1.5 la medida entre los cerros El Mirador y La Calavera; las cantidades por el tipo de medida kilómetros son 20 y x, 20 representa la equivalencia del segmento (por cada dos centímetros son 20 kilómetros) y x la cantidad de kilómetros que se deben de buscar parea emitir la respuesta de la distancia real aproximada de kilómetros que hay entre esos dos cerros.

Lo anterior corresponde a la consigna del inciso a (ver primera imagen), con el entendimiento que 2 cm equivale a 20 km, se ejecuta la medición como se ejemplifica en la figura de enfrente. La distancia (1.5 cm) es el tercer elemento, su acomodo debe ser bien comprendido por el alumno; así se cumple que haya dos tipos de medida distintos, su correspondencia que llaman biyectiva, término matemático de correspondencia algo no fácil de digerir en educación primaria por lo que no se ahondará y se representa en el esquema anterior.

Se sugiere que esta relación multiplicativa, que es la más sencilla de abordar, se ejecute mediante la aplicación de un esquema (tabla) fácil de manejar para un niño de primaria, en el esquema se debe ver claro los tres elementos que nos llevan al resultado esperado. La lección 17 permite explorar el desafío y partir hacia el resultado conociendo el valor unitario de la medida que muestra la incógnita y el empleo de una multiplicación.

En el uso de un esquema se muestra que mediante una multiplicación paralela vertical y otra paralela horizontal se encuentra el resultado. En el caso del esquema de arriba (multiplicación horizontal) nos muestra un operador (x 10) que nos lleva de una medida a otra aunque sean (las medidas) de naturaleza distinta sin importar que representen distancia. Este operador representa una función y nos lleva a entender el paso de una categoría (en este caso centímetros) a otra categoría (kilómetros)

Cuando se hace una operación multiplicativa como se muestra en la imagen de enfrente, de manera vertical, también se puede encontrar la respuesta. Conociendo el valor unitario se puede encontrar el operador que nos lleve a la medida que encontramos en el dibujo entre los dos cerros, se dejan ambas medidas y sus respectivos operadores (1.5 y .75), a este proceso donde se pasa de una medida a otra medida de la misma categoría se conoce como como operadores sin dimensión o escalares y es imprescindible que no se confundan ambos procesos.

Sólo se muestra otro ejemplo pues se considera entendido el proceso. En la consigna d se pide encontrar la distancia en kilómetros entre los cerros Los Gallos y San Juan, la figura nos muestra que hay una distancia de 4.5 cm, con el esquema se puede encontrar la respuesta como se aprecia en la figura siguiente donde se comparan los dos procesos ya estudiados.

Esta primera forma es la más sencilla pero primordial para entender posteriores relaciones multiplicativa que se irán incorporando conforme se observen otros desafíos, por lo pronto este antecedente es importante para resolver el desafío siguiente (el número 18).