En el presente desafío se narran dos problemas donde se pide al alumno que realice una serie de comparaciones, y de hecho desde el desafío 49 del libro de sexto grado se plantean ejercicios similares. La intención es que resuelva el actual desafío acudiendo a las similitudes que pueda tener con las consignas ya trabajadas en el dicho desafío 49... mientras que en el anterior se pretende que realice comparaciones sin acudir tanto o nada a operaciones ya que son números manejables para un alumno de sexto y sobre todo ponga atención al último problema con el distractor de las naranjas, en el desafío 50 presente aumenta la complejidad al manejar razones efectuando equivalencias.
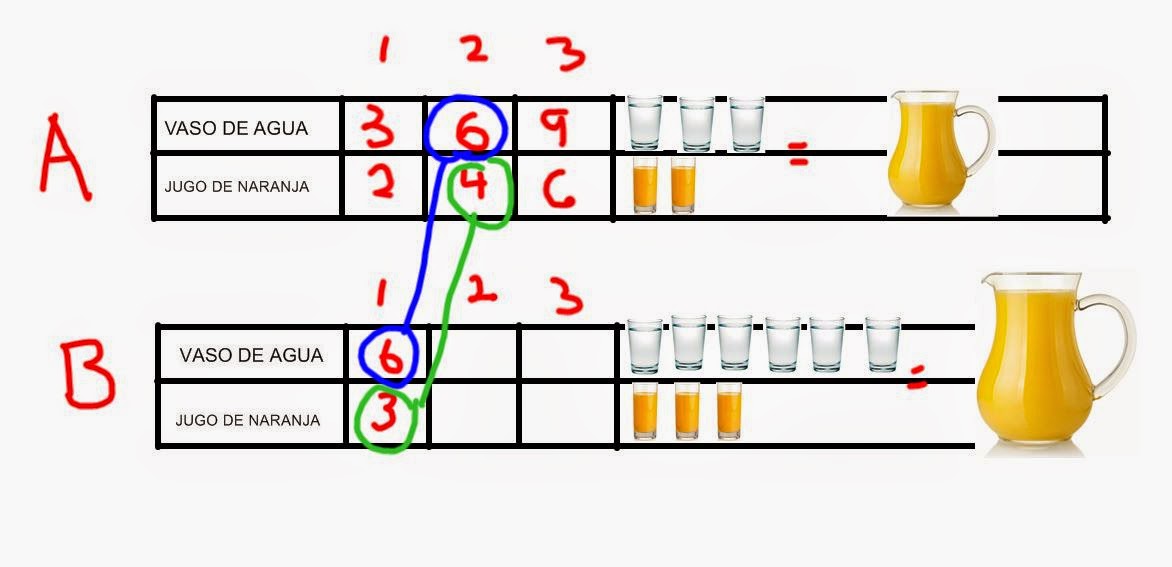El primer problema que se encuentra en la primera figura nos lleva a centrarnos en la cantidad de jugo que se vierte en cada preparación. Primero gráficamente tal como se muestra podemos comparar que si se usara la misma cantidad de agua en la bebida A y en la bebida B, para la bebida A se emplearía un vaso más de jugo, lógico eso añadiría más sabor a la bebida A. En el cuadro siguiente se ejecuta o muestra cómo se podría comprobar esto si se acude a realizar operaciones. 
En el cuadro se muestran dos fracciones resultado de un acomodo bajo el siguiente criterio, se anota 2/5 y 3/9 porque al buscar en que porcentaje es más intenso el sabor de naranja independiente de la cantidad de líquido en cada preparación, el numerador representa la cantidad de vasos de naranja y el denominador la cantidad de vasos empleados para cada bebida.
Si se observa, el porcentaje de jugo de naranja es mayor en la primera combinación, el distractor para algunos alumnos puede ser la cantidad de líquido, la jarra de la medida A contiene menos líquido que la jarra de la bebida B, pero el concentrado de sabor naranja es mayor en uno que en otro.
En lo que respecta a la segunda tarea, se debe concentrar de nuevo en la pintura azul, de la cantidad total que se mezcle entre pintura blanca y azul, el tono azulado debe ser más fuerte en uno o en otro dependiendo del porcentaje empleado, recurriendo a un proceso análogo al primero,
Se observa que para la fachada el total de botes de pintura es 12, y para el cuarto el total de botes de pintura es 5. Al observar la imagen y haciendo un comparativo, se percibe que por cada 2 botes de pintura blanca en la fachada se emplean 4 de azul y por cada 2 botes de pintura blanca en el cuarto se usan 3 de azul... desde aquí el alumno debe empezar a percibir que el tono en la fachada debe ser poco más intenso.
En esta imagen no se anota el porcentaje, pero si el alumno ya está avanzado en este aspecto, concluirá que de 5 botes de pintura mezclados, cada bote aporta un 20% del total independiente de la cantidad que se obtenga y en el caso de los doce botes, cada uno representa el 8.333...%. La mezcla de la fachada tiene un 66.66...% de azul, mientras la mezcla para la habitación contiene un 60%, en la realidad puede resultar imperceptible la tonalidad pero con las operaciones se puede establecer la diferencia.
Hasta este momento se observa cómo las múltiples estrategias que pueden emplearse para las operaciones aditivas o multiplicativas así como para el uso de la fracción se entretejen dejando la frontera entre uno y otro imperceptible, lo interesante es la pretensión de los desafíos que el alumno exponga sus conocimientos y tenga diferentes caminos para llegar a la solución de las tareas. Al usar dos fracciones y establecer lógicamente por qué se anotan de esa manera y no de otra, una estrategia empleada fue la comparación de producto cruzado, así en el caso de la naranjada se estableció que 2/5 es mayor que 3/9 y 8/12 mayor que 3/5... en fin recordar que se propone lo anterior como sugerencia independiente de las estrategias que en las consideraciones previas se realicen.
No hay comentarios:
Publicar un comentario