La quinta y sexta categoría es el
tema que se tratará en este escrito, se manejan así ya que más adelante el
lector verá cómo esquemáticamente se usan en el primer caso la transformación
de dos número relativos y en el segundo la composición de números relativos. El
manejo de este tipo de números requiere su identificación como número o
negativo o positivo en cada óvalo de esquema propuesto construido por G.
Vergnaud que son trabajados o aludidos
tanto por María Luisa Ruiz Higueras y Juan Miguel Belmonte Gómez en el texto La
Didáctica de las Matemáticas (2006) y Nunes y Bryant en el Texto Las matemáticas y su
Aplicación (2002).
Los tipos de problemas que se
plantean, generarán múltiples situaciones dependiendo de la ubicación de la
interrogante, además de la situación positiva o negativa tanto en los datos
planteados como en la misma respuesta. Entonces situaciones e invariantes
estarán presentes aquí; qué situaciones se están aludiendo, la primera de
transformación en la quinta categoría donde un estado relativo da lugar a otro
estado relativo y de composición u ordenación entre dos estados relativos en
otro en el caso de la sexta categoría. Podrá el lector encontrar similitudes
con las primeras categorías, pero a de preverse que aquí se manejan números o positivos
o negativos.
Se debe entender también que entran
en juego lo que Vergnaud llama las invariantes operatorias, es decir, las
operaciones del pensamiento que ejecuta el alumno y cristaliza manual, gráfica
o en papel. El esquema, en este caso a lo largo del blog donde se han trabajado
las categorías, se han presentado precisamente para que el docente las
comprenda y didácticamente (a modo de sugerencia) trabaje con sus alumnos como
una organización invariante para resolver problemas.
Entremos entonces al análisis de
algunos problemas en sus respectivas categorías.
1. Quinta categoría: su similitud con la segunda categoría nos harán
inferir que hay 6 formas de problematizar, pero en realidad el número aumenta
dependiendo el carácter positivo o negativo como enuncia Belmonte.
Situación: Para sembrar Abundio
consiguió varias veces dinero con José, haciendo cuentas se fijó que le debía $
700, como fue un mal año acordó pagarle $ 500, ¿Cuánto dinero le sigue debiendo a
José?
El esquema para este problema es el
verde, muestra un resultado negativo al responder la pregunta, ha de entenderse
(y en esto entra la comprensión lectora) que nos estamos refiriendo a la acción
que se está ejerciendo en Abundio. Se anota -700 en el estado relativo inicial
porque de entrada para sembrar y cosechar tuvo que endeudarse con 700 pesos, al
tener dinero en sus manos (que no se dice cuánto) optó o acordó regresarle 500
pesos a José por lo que en el esquema se representa positivamente, de esta
manera no entra en contradicción con la cantidad relativa que adeuda inicialmente
y que reconoce que aún seguirá debiendo 200 pesos (-200) a José.
Aprovechando los datos para
entenderse alguna de las múltiples variantes posibles a presentarse, podemos
redactar la situación de la siguiente manera: Para sembrar Abundio consiguió varias
veces dinero con José, haciendo cuentas se fijó que le debía $ 700, como fue un
mal año acordó le regresa una cantidad de dinero acuerdan que seguirá debiendo
200 pesos, ¿Cuánto dinero le entregó Abundio a José?
Esperando se entienda la intención,
se pide que observen el esquema de color anaranjado y analicen la misma
distribución de cantidades y reconozcan en la transformación de los dos estados
relativos la incógnita.
Finalmente y con la misma situación
y datos se ejemplifica para entender el planteamiento de la incógnita en el
estado relativo uno o inicial. Para sembrar Abundio consiguió varias veces dinero
con José, haciendo cuentas se fijó que aún con los 500 pesos que le debía,
seguía habiendo un adeudo de 200 pesos, ¿Cuál es entonces la deuda original que
hubo entre Abundio y José?
NOTA: Se puede dar clic en el
dibujo o gráfico, los llevará a un enlace donde está elaborado bajo formato Excel,
cuenta con esquemas para las seis categoría que puede emplear para sus
problemas que localice en los libros de texto para alumnos de primaria, las
celdas donde puede introducir datos están abiertas a excepción del resto del
documento para que no alteren las funciones que deseo preservar. Si se
encuentra una inconsistencia favor de comentarla y si sabe la forma de
corregirla agradecería me indicara cómo.
2. Sexta categoría: Podría decirse que es similar a la tercera
categoría, pero se advierte que en este esquema los números que entran en juego
son o positivos o negativos como en la categoría anterior, mientras que la
tercera sólo en la relación se daba el caso de señalar que el número era
positivo o negativo.
Situación: Ana compra a crédito el
mandado del diario en la tienda de don Polo, al final de la semana se da cuenta
que ya le debe 450 pesos, pero a su vez don Polo le debe 500 pesos a Ana porque
le cortó el pelo y le lavó su ropa, Ana entonces tiene dinero a su favor, ¿Qué cantidad
le debe a Ana el tendero?
Al igual que en la categoría
anterior, se ha de analizar que el protagonista inicial es Ana y sobre ella
versan los datos aunque entre otro personaje, la pregunta se establece según el
planteamiento en el estado relativo que van a componer las dos situaciones
presentadas (debe (-450) pero también le deben (+500)) mostradas en el relativo
1 y 2 respectivamente por eso se concluye que tiene 50 pesos a favor, ver
esquema rosa.
Si la pregunta se plantea para la
situación relativa 1 (esquema naranja), podría entre otras formas enunciarse
así: Ana compra a crédito el mandado del diario en la tienda de don Polo, al
final de la semana se da cuenta que debe
pagar, pero se acuerda que a su vez don
Polo le debe 500 pesos porque le cortó el pelo y le lavó su ropa, Ana entonces
tiene dinero a su favor y le dice al tendero que son 50 pesos, ¿Qué cantidad le
debía entonces Ana al tendero por el mandado del diario?
Y para entender porque la pregunta
se puede trasladar al relativo 2 (esquema verde), entonces la redacción a la situación sería
así: Ana compra a crédito el mandado del diario en la tienda de don Polo, al
final de la semana se da cuenta que ya le debe 450 pesos, cuando va a pagar,
don Polo le entrega 50 pesos a Ana porque le cortó el pelo y le lavó su ropa, ¿Cuál
es la cantidad le debía a Ana el tendero por sus servicios?
Esperando cumplir sus expectativas
respecto al tema, se ponen a su disposición los esquemas en el enlace
respectivo.
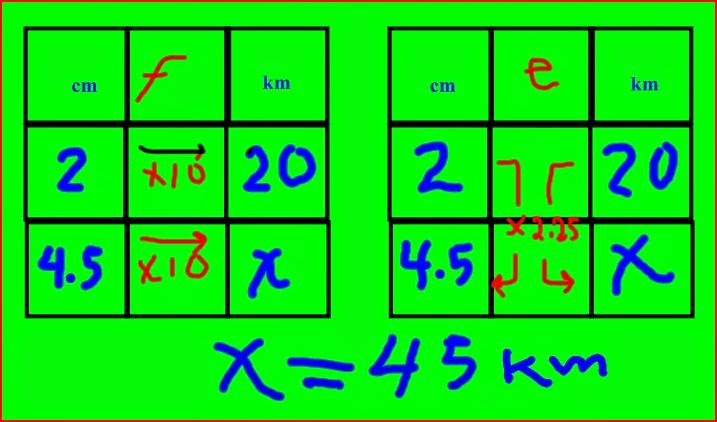
 La correspondencia entre las medidas se hace de manejo
sencillo con el esquema propuesto en el desafío 17 también de sexto grado ya
que de entrada al leer la tarea nos señala claramente el valor unitario de cada
producto.
La correspondencia entre las medidas se hace de manejo
sencillo con el esquema propuesto en el desafío 17 también de sexto grado ya
que de entrada al leer la tarea nos señala claramente el valor unitario de cada
producto.  Podemos describir el proceso en las dos formas; mediante una
multiplicación del factor (de manera horizontal) entre la unidad de medida de longitud
(metros) por el valor en pesos de la unidad de medida anterior. Entender como
factor pues nos permitiría entender por qué una unidad de medida (A) al operar
se transforma en otra unidad de medida (dinero) que se corresponden.
Podemos describir el proceso en las dos formas; mediante una
multiplicación del factor (de manera horizontal) entre la unidad de medida de longitud
(metros) por el valor en pesos de la unidad de medida anterior. Entender como
factor pues nos permitiría entender por qué una unidad de medida (A) al operar
se transforma en otra unidad de medida (dinero) que se corresponden.