Los problemas de tipo aditivo: composición de medidas... primera categoria

Los problemas de tipo aditivo: composición de medidas.

Hurgando en algunos textos enfocados en el estudio y análisis de problemas que impliquen el uso de la adición (y sustracción) para encontrar su solución, me encuentro información que confrontada nos lleva a la una misma fuente, a la teoría que plasma en su libro El niño, las matemática y la realidad, escrito por Gérard Vergnaud en el capítulo Los problemas de tipo aditivo, nos muestra las seis categorías de relaciones aditivas que se presentan cuando se plantean problemas a los niños en la escuela primaria. De manera somera, en un blog anterior inicié el tema que es retomado con el afán de mostrar más información al respecto.

En este trabajo se centrará en la primera categoría y sus dos tipos de planteamientos que se presentan. Primero, es necesario señalar que Terezinha Nunes y Peter Bryant en su texto Las matemáticas y su aplicación: la perspectiva del niño, cuenta con interesantes planteamientos aunque estos autores dicen en el libro difieren en algunos aspectos pero que aquí no se tratarán, sino que se contrastarán las aportaciones.

La primera categoría enunciada por Vergnaud es: dos medidas se componen para dar lugar a otra medida, y aclara que todas las relaciones aditivas son a la vez relaciones ternarias, esto es cuando tres elementos se relacionan entre sí… y por tanto en las adiciones puede haber diversas estructuras que surgen de los planteamientos. Entonces en esa relación de la primera categoría intervienen únicamente medidas y el resultado es por tanto otra medida. Es pertinente recordar que sólo los números naturales pueden representar una medida y en los esquemas se representará con un rectángulo.

Aquí es primordial acudir a las aportaciones de Nunes y Bryant quienes investigaron al respecto con niños de los primeros grados y de preescolar en Brasil. Las coincidencias con Vergnaud son los que ellos llaman situaciones parte-todo donde no opera ninguna trasformación, sino que las medidas son parte de un mismo universo y no se necesita hacer alguna trasformación que es característica que se observa a partir de la segunda categoría y que en este trabajo no se analizará. 

A los problemas o situaciones que se pueden representar en esta categoría fue llamada los números como medidas estáticas y coincide que se puede plantear dos formas de problemas, la primera donde se mencionen las (dos) partes y se pide que encuentre el todo como respuesta y la segunda donde se les dice el todo y un dato de una parte para que encuentre la respuesta en el segundo dato de la parte.

En los problemas es común emplear cantidades continúas y es fácil reconocerlas como medidas, pero también las cantidades discretas o paquetes que conforman un conjunto son medidas que nos permiten encontrar o conocer el tamaño de dicha colección.

Juan Miguel Belmonte Gómez en el quinto capítulo del libro Didáctica de las matemáticas se adentra en el estudio de los problemas aditivos y sustractivos. Llamó a esta categoría problemas de composición de medidas, en los ejemplos que Nunes y Bryant se ejemplifican esa relación parte todo con elementos homogéneos, es decir, la medida 1 y la medida 2 son elementos iguales que únicamente cambia una característica ya sea el color o tamaño pero siguen perteneciendo a una misma campo y Belmonte agrega que en esta categoría se pueden incluir en los problemas elementos heterogéneos y que en el resultado se agregue el hiperónimo del conjunto. Ejemplo de homogeneidad: medida 1 X peces verdes, medida 2 X peces naranjas… da lugar a un todo donde se emplee  la palabra peces en el resultado. Ejemplo de heterogeneidad: medida 1 X  guajolotes, medida 2 X caballos… da lugar a un todo donde al resultado se añade la palabra animales.

Entonces estamos de acuerdo a la primera categoría se puede encontrar dos tipos de problematización, y es la forma más común de plantear desafíos a los alumnos… de allí la importancia que el docente conozca y trabaje este tipo de problemas donde se implica sólo el uso de números que representan medidas y no requiere trasformaciones, con madurez poco a poco introducir estrategias sustractivas pero siempre empleando elementos gráficos acompañado posteriormente del uso de operaciones. Se ejemplifica con problemas donde se usan números pequeños sólo para entender la mecánica que debe llevar a apropiarse de los conceptos y procesos donde se emplean MEDIDAS.

1. Problemas donde la respuesta a la pregunta es el resultado (EL TODO) de la suma de dos medidas (primer tipo de la categoría 1)

 

·         En una pecera hay 7 peces naranjas y 6 peces verdes, ¿cuántos peces hay en la pecera?

·         Dentro de un corral se encuentran 7 guajolotes y 6 caballos, ¿qué cantidad de animales hay en el corral?

En este primer tipo de preguntas están claramente establecidas las medidas y por supuesto se observa que son contables, su resultado también es una medida, se cumple la ley de composición que es la adición de dos números naturales… dos números que representa algo contable y cuyo resultado los aglutina… 13 peces o 13 animales; peces naranjas + peces verde = peces  y guajolotes + caballos = animales. Belmonte dice que es el tipo de problemas que se les presenta casi siempre por primera vez a los niños, pero desafortunadamente al aplicarles un ejercicio por lo regular se incluyen o plantean situaciones donde necesariamente deba realizar transformaciones sin antes haberlas trabajado.

 2. Problemas donde la respuesta  a la pregunta es el resultado (UNA PARTE DEL TODO) de la suma de dos medidas (segundo tipo de la categoría 1)

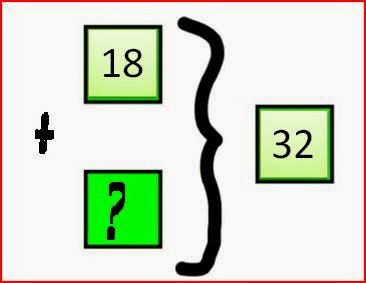·         De los 32 miembros de mi familia que viven en La Comarca, a 18 miembros les gusta el fútbol y le van al Santos y el resto el béisbol y apoyan a Vaqueros, ¿qué cantidad de miembros les gusta el béisbol y apoya a Vaqueros?

Comprender que se trata de un todo o universo donde hay dos grupos o partes es la parte primera que se debe entender en el planteamiento, de allí pasar a buscar la solución representando a cada miembro en su respectivo grupo… con bloques físicos, figuras, piedras o cualquier material; posteriormente el uso de la operación. La forma más económica para un adulto o alumno avanzado es realizar una sustracción, pero es importante trabajar la adicción y que la resta sea un descubrimiento inducido por el maestro, es decir, sabemos que la respuesta rápida y deseable sería una resta (32 – 18 = x), pero lo adecuado primero es una adición con huecos como dice J. Miguel Belmonte (18 + x = 32) para que averigüen mediante representaciones. La resta sería cuando ya se domina el proceso y se comprende la relación que existe con la suma.

Como ya se mencionó, si el alumno acompañado del docente trabaja y comprende las dos posibilidades donde consigue la respuesta al leer un desafío que se trata de problemas de tipo aditivo de la categoría uno, entonces podrá aumentarle la complejidad de acuerdo a su grado.

Espero sea de utilidad la información plasmada en el presente trabajo.